Something odd
 The molecules
all started from the same point, roughly the center of the box, with random
initial velocities. They then spread out, bouncing around, just like the
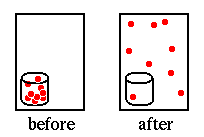
molecules in a small bottle (e.g. a bottle of perfume) would escape if the
bottle were opened and fill up a room [illustration at right]. Indeed, what
you were looking at is considered to be an excellent model of what a real
gas looks like under very high magnification.
The molecules
all started from the same point, roughly the center of the box, with random
initial velocities. They then spread out, bouncing around, just like the
molecules in a small bottle (e.g. a bottle of perfume) would escape if the
bottle were opened and fill up a room [illustration at right]. Indeed, what
you were looking at is considered to be an excellent model of what a real
gas looks like under very high magnification.
But curiously the model "gas" in this applet after a while suddenly compresses itself right back to its initial state. This is in drastic contrast to what you would expect to see for a real gas. That is, were we to reverse the ``before'' and ``after'' labels on the illustration above, you would immediately conclude that the process illustrated was not natural. It could not occur spontaneously, and could only occur at all if caused by some external force.
So what's going on?
One of the most difficult philosophical points of statistical mechanics has always been that simple mechanical systems -- say a molecule or two bouncing around in a closed box -- quite clearly exhibit ``reversible'' behaviour. That is, were you to film such a system and then run the movie backwards, the film would not look unusual. One would find it impossible, in general, to distinguish such a ``reversed'' film from a ``forward'' film of the same molecules under the same forces, but starting from slightly different initial conditions. Assuming we observe the system often enough so that we see it starting from most of its possible initial conditions, then any behaviour that appears in a ``reversed'' film will also be seen in a normal, ``forward'' film of the system.
And yet: clearly the behaviour we observe in large, complex objects is not reversible. If you ``run the movie backwards'' after you film people, cars, or weather you get Buster Keaton and Charlie Chaplin, big laughs, certainly not anything resembling reality. Molecules moving ``forwards'' or ``backwards'' along their trajectories might well be equally plausible, but it seems clear that people, the atmosphere and automobiles move essentially always in one direction along their trajectories: automobiles never produce gasoline from exhaust and water, rain does not rise to the clouds, and (alas) none of us is getting any younger.
Boltzmann's Paradox
![[Boltzmann's picture]](boltzmann2.jpg)
This problem is sometimes called (among statistical mechanics) Boltzmann's paradox, in part because Ludwig Boltzmann [that's he at right], one of the architects of modern statistical mechanics, and a giant among scientific minds, struggled with this issue at the close of the last century. He endured a storm of criticism among the scientific and philosophical community for his efforts to solve the paradox in favor of the simple, mechanical model of matter that is modern atomic theory, and died (by his own hand) an extremely bitter man.
Boltzmann's solution to the paradox of irreversibility is in many ways as drastic and astonishing as Einstein's solution to the paradox of privileged frames of reference, which led to relativity. Indeed, Boltzmann asserts that the paradox is resolved not (as would be the most natural guess) by some delicate irreversibility of microscopic atomic motions, that only becomes significant and observable when zillions of atoms conspire to produce macroscopic phenomena; rather Boltzmann asserts that the paradox is resolved by the fact that macroscopic phenomenon are not in fact irreversible! They merely appear that way. To put this bluntly: any macroscopic cause and effect not only can but must operate equally well backwards as forwards: that the forest fire spontaneously produces smoke and ashes from trees necessarily implies that under the proper initial circumstances smoke and ashes will spontaneously form living trees.
How can this rather peculiar assertion be reconciled with reality? By the observation that the number of different ways in which molecules can ``reverse cause and effect'' is enormously smaller (and hence fantastically less likely) than the number of ways in which they can trace out the normal ordering. For example, there are enormously many ways in which molecules might spontaneously rearrange after lightning strikes a tree, all of which would be interpreted macroscopically as ``the tree begins to burn.'' By contrast there are hardly any ways -- there need not be more than one to satisfy Boltzman's assertion -- in which molecules of a burning tree might spontaneously rearrange in a way that would be interpreted macroscopically as ``smoke and ash recombine to form wood.'' And let us stress that when we say ``enormously many'' we are not speaking lightly --- the numbers involved are so large they are impossible even to write down. The number of atoms in the entire Universe or seconds since the Big Bang is essentially zero by comparison.
Because of the huge number of ways in which ``normal'' events can occur, compared to those in which ``reversed'' events can occur, if we observe ever so many times lightning striking strees, we will see uncounted variations on the theme of wood turns to smoke and flame, but many many lifetimes of the Universe are likely to go by before we see the one, peculiar result of a tree reconstituting itself from smoke and flame. Being limited to human lifetimes of experiments, we have naturally concluded from our collective experience that the burning of trees is ``irreversible'' rather than, as in fact it is, merely awfully unlikely to undo itself.
The simulation
But if you watch the simulation for a while, you will discover that Boltzmann was right. All the atoms will eventually come precisely back together again in the middle of the box, spontaneously retracing exactly their initial steps and completely reversing the original ``irreversible'' expansion. (You may also notice the formation of some unnatural-looking partially ordered states before the final collapse.)
Why does this happen? Since any closed system has a certain finite number of states in which it can exist, if you wait long enough the system will have to return to any state you care to name. The maximum time this takes is called the Poincaré recurrence time, and of course for most systems it is unbelievably large. But for this peculiar system, it turns out to be quite short. So short, in fact, that the unusual initial state (all the atoms at the center) necessarily recurrs on a time scale that is observable. The recurrence of the initial state is not "programmed" into the simulation by a clever choice of the initial conditions -- each time you start the simulation the initial velocities are randomly chosen. The recurrence is observed simply by the fact that this system exhausts rather rapidly its entire repertoire of possible states and must then begin repeat visiting them.
Incidentally, if you are wondering why this system has such as small number of possible states, it's because the initial velocities of the particles are all integer multiples of one another.
Statistical Mechanics
The area of research of statistical mechanics is occupied by people from many backgrounds and disciplines, but physical chemists play one of the leading roles, and professional training in physical chemistry is an excellent way to prepare to take on an active part in the remarkable science of understanding complexity.
References
Physical Chemistry Faculty at UCI, folks doing research in statistical mechanics.
Chem 130C, the first undergraduate course in statistical mechanics given by the Department of Chemistry at UCI.
ChemE 532, the first graduate course in statistical mechanics given by the Department of Chemical Engineering at UT Knoxville.