What's happening?
Otherwise you saw a realization of one of the classic formal problems in quantum mechanics: the particle in a box. Imagine that a very small, light particle like an electron is trapped in the box formed by the thick black borders on the previous page. The principles of quantum mechanics tell us that the total energy of the particle in this box must change in fixed, discrete (quantum!) leaps. The RED horizontal lines drawn across the box show the energies a particle in this box can have. The height of each line above the box floor corresponds to the value of the energy: a higher line means a higher energy.
The primeval quantity in the simplest formulations of quantum mechanics is the wavefunction. This beast tells you everything you can know about the particle. In particular the square of the wavefunction tells you the probability of finding the particle as a function of position. The BLUE lines on the previous page show the wavefunctions that correspond to each allowed energy. Just so that the wavefunctions don't lie on top of one another, and to allow you to easily match a wavefunction with its corresponding energy, each wavefunction is drawn with its x-axis lying along the red line indicating its energy.
Take command!
As you introduce and modify this new feature of the box the mighty Java engine underlying this deceptively simple picture will automatically and continuously recalculate and redisplay the allowed energies and corresponding wavefunctions of the system. Hopefully that will strike you as it strikes us as way cool.
It's interesting that this system can be solved exactly. The allowed energies and wavefunctions you see are all exact -- no approximations are made! What's also interesting is that you can, by manipulating the pedestal appropriately, explore many of the most basic concepts and phenomena in quantum mechanics, including degeneracy, quantum tunneling, tunneling splitting, and the ordering of wavefunctions by their "nodes". You can also explore smoothly the crossover from the simple particle in a box system you see initially to one of the most famous quantum systems of all: the double well. J. J. Sakurai has commented that four Nobel prizes -- including that for lasers -- were the result of considering the properties of various double well systems.
Experiment!
Some notes on performance
To return to the starting situation, if the applet gets confused, you can try pressing the Reload button on your browser while holding down the Shift key at the same time. If the applet does truly strange things, though, please contact the author so he can try to fix them.

Some notes about quantum mechanics
What's a wavefunction?
The wavefunction is a strange mathematical beast. One can look at it in many ways. One way is to say that particles of solid matter can be considered, as Mr. Spock might say, to be stationary waves in the very fabric of space, and a wavefunction simply describes this wave.
Say what? I'm a doctor, Jim, not a quantum mechanic. . .
Okay, if you swish your hand around in the bathtub, you'll note that the only waves that persist for a long time are those that "fit" inside the bathtub, in the sense that a whole number of waves, measuring from crest to crest, fit into the bathtub.These waves are called "standing" waves because, well, they just stand around instead of travelling forward like waves at the beach. In other words, they have their crests and troughs always in the same places, and the areas midway between the crests and troughs (the "nodes") where the water level is undisturbed also always in the same places.
Here's the largest possible bathtub wave, which has a crest at each end:

Here's another, which has a crest at each end and in the middle: 
The possible energies of standing waves in the bathtub are limited to certain, specific (quantum!) values by the requirement that each wave fit exactly into the bathtub.
Now the energies of the bathtub waves, like the wavefunctions of the particle in the box, increase with the number of wave crests that fit into the tub. If you swish the water very gently and slowly, for example, then the only wave you'll see will be the ``sloshing'' wave that has a crest exactly at each end of the tub and a node in the middle. As you increase your agitation -- whee! -- you'll see waves that have more and more crests in the middle, at least until you slop all the water out onto the floor. . .
The wavefunctions you see on the previous page are sort of like the standing waves in the bathtub. In fact, the allowed energies are calculated pretty much by figuring out which waves "fit" into the box, as noted below. The meaning of the peaks and troughs of the wavefunction is somewhat like the waves in the bath, in the sense that something is going on at the peaks and troughs but not at the nodes. In the case of wavefunctions, the square of the wavefunction at any point is equal to the probability that the particle is at that point: hence the particle is likely to be found at peaks or troughs in the wavefunction, and is never found at the nodes.
Kinetic energy
The energy of the particle in the box is partly potential energy, which you might interpret as energy which is not yet ``realized'' as motion but could be. We can read off the potential energy of the particle at any point in the box by looking at the level of the floor of the box at that point. A higher level means a higher potential energy.The rest of the energy of the particle is kinetic energy, which is to say the energy of its actual motion. The faster the particle bounces around the box, the larger its kinetic energy.
How is the kinetic energy reflected in the wavefunction? It turns out the kinetic energy of the particle at any point is just equal to the relative magnitude of the curvature of the wavefunction at that point. (This is true for real waves as well -- the water is moving fastest where the wave is most sharply curved, which is at the very tip of the crest.) You can see that wavefunctions at higher energies must be more sharply curved on average, because that gives a shorter distance between successive wave peaks and hence more wave peaks fitting into the box. This reflects the physical fact that to increase the energy of the particle in the box we must increase its kinetic energy, since the potential energy is fixed by where the floor of the box is. The average kinetic energy of the particle for any of the allowed total average energy is just the difference between the red line and the floor of the box.
Now the curvature of a function is just the change in slope of the function as one moves from left to right through any point. Since the slope of a function is its first derivative, the curvature must be the second derivative. [Calculus rears its ugly head! You can click here to skip the math that follows.]
That is, if we represent the graph of the wavefunction by a function 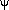 (x),
then the curvature of this graph is given at any point x by:
(x),
then the curvature of this graph is given at any point x by:
---- dx2 |
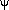 (x) (x) |
| [ [ [ |
---- dx2 |
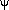 (x) (x) |
] ] ] |
÷ | 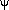 (x) (x) |
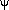 2, like so:
2, like so:
| K(x) = | --- 2 |
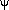 (x) (x) |
---- dx2 |
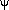 (x) (x) |
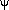 went into canceling
the denominator in the previous expression. We put the ½ in here just
to make the units come out conveniently. You could define units of energy
where this constant would not appear, if you wanted to.
went into canceling
the denominator in the previous expression. We put the ½ in here just
to make the units come out conveniently. You could define units of energy
where this constant would not appear, if you wanted to.
The Schrödinger Equation
If we add to the kinetic energy at any point the average potential energy of the particle at this point, we'd have the complete average energy at point x. Let the potential energy at a point x be given by the function V(x). Then the average potential energy at x is V(x) multiplied by the probability that the particle is actually at x, like so: V(x) 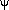 2(x)
2(x)
Putting the kinetic and potential energy terms together we have the complete average energy at any point x:
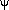 (x) (x) |
[ [ [ |
--- 2 |
---- dx2 |
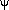 (x) + V(x) (x) + V(x) 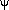 (x) (x) |
] ] ] |
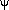 from each
term. If we sum (i.e. integrate) this expression over all positions x
we will have the total average energy of the particle:
from each
term. If we sum (i.e. integrate) this expression over all positions x
we will have the total average energy of the particle:
| E | = | dx | 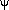 (x) (x) |
[ [ [ |
--- 2 |
---- dx2 |
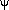 (x) + V(x) (x) + V(x) 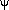 (x) (x) |
] ] ] |
Now, we have a great principal of mechanics which tells us what the wavefunction will be if we have an expression for the energy. The fancy name for this principle is the variational principle, which can also be considered as no more than the second law of thermodynamics in disguise. A simpler name might be the ``Principle of Laziness.'' The idea is simply that the wavefunction adjusts itself until the particle has the least possible total average energy.
It can be shown that the right-hand side of the expression for the energy above will be a minimum if and only if the expression in brackets is given like so:
--- 2 |
---- dx2 |
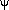 (x) + V(x) (x) + V(x) 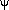 (x)
= E (x)
= E 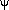 (x) (x) |
Boundary conditions and quantization
You can solve the Schrödinger equation numerically quite easily. You just start somewhere where you know the wavefunction; for example we know that the probability of the particle being inside the left wall must be zero, since if it were not the potential energy of the particle would be infinite. So we can start at the left wall, and require the wavefunction to be zero there. Then we pick out any old initial slope for the wavefunction. Now we use the Schrödinger equation to calculate the curvature of the wavefunction at this point. That tells us how the curvature changes, so we can now calculate the slope a little bit further on. And the slope itself tells us how the wavefunction changes, so now we can calculate the wavefunction a little further on. We're OK in this process as long as we don't try to jump ahead too fast. We have to "integrate the differential equation" a tiny step by a tiny step. The precise reason for this is that we don't have an equation for the change in the curvature, that is, we don't know the third derivative of the wavefunction. However we do know that the contribution of the nth succeeding derivative to the change in the wavefunction is proportional to the distance we are trying to move ahead raised to the nth power (this is Taylor's theorem). If we keep this distance small then when it is raised to the nth power it gives essentially zero.If we use Schrödinger's equation we can generate a wavefunction for any energy whatsoever. Where the quantization of the energy comes in, that is, the forbidding of all but certain values of the energy, is that we have to make sure that the wavefunction reaches a certain value at the boundary of the problem. This is a "boundary condition", and it is to these that the wavefunction owes its quantum nature, just as the walls of the bathtub enforce the quantization of waves there, as indeed the open sea would not.
In the case of the square well, our boundary condition is that the wavefunction be zero as soon as it reaches the right-hand wall. If we require this, it turns out we can only choose certain specific values for the initial slope and curvature in slope of the wavefunction at the left-hand wall. This in turn means we can only use wavefunctions corresponding to certain energies. Quantization of the energy!
Classically forbidden zones
When you raise the pedestal high enough that the top is higher than an allowed energy, then a particle having this allowed total energy is forbidden in classical (nonquantum) mechanics from being inside the pedestal region. The reason is clear: the potential energy at a point in this region is greater than the allowed total energy at this point, hence the particle if it were here would have to have a negative kinetic energy. This makes no sense classically, because you cannot, classically, have kinetic energy less than that implied by zero motion (which is zero).But not quantum mechanically. Quantum mechanics only requires that the total average energy summed up over all possible positions of the particle be equal to the total average energy. It's OK to have a negative kinetic energy at some point as long as it's balanced by a positive contribution somewhere else. Thus the quantum particle is allowed to visit "classically forbidden" regions of the box, i.e. those inside the pedestal when the top of the pedestal exceeds the total energy. You will note, however, that the wavefunction is greatly damped in these regions, and more so as the top of the pedestal is raised further, indicating that the probability of the particle being in a classically forbidden region is greatly reduced.
This gives rise to the famous phenomena of quantum tunneling. Suppose a particle is trapped in a well, as in, say, one of the two wells you create by raising the pedestal high. Quantum mechanics says the particle can get into the pedestal even if that region is classically forbidden, as you can see by doing the experiment on the previous page and looking at the wavefunction.
Now if the classically forbidden region is of a finite width, and there is a classically allowed region on the other side (as there is in this system, for example), then a particle trapped in the first allowed region can be found after a while in the other side, having apparently traversed a region of space in which it was "not allowed". This is "tunneling", so named because one imagines the particle tunnneling through the barrier offered by the pedestal, say, instead of going over the top, which it can't do because it doesn't have enough energy.
Radioactivity
Tunneling underlies a great many interesting phenomena. For example radioactive decay: a proton or neutron is quite happy inside the nucleus because it is strongly attracted to the other neutrons and protons there. Outside of the furnace inside the Sun or a nuclear bomb, protons and neutrons do not have enough energy to get away from this mutual attraction. That is, the classically allowed region inside the nucleus is surrounded by classically forbidden prison walls.But interestingly the force binding protons and neutrons together falls off very rapidly with distance (unlike gravity, say, or a magnetic field). Hence there is a certain point, not far from a nucleus, where protons and neutrons are once again classically allowed. Thus a tunneling situation exists, with the barrier between the inside and the outside of the nucleus being the attraction of any given proton or neutron for all the rest inside the nucleus.
And indeed, on regular occasions groups of protons and neutrons are observed to tunnel out of the nucleus -- that is, the nucleus undergoes radioactive decay -- at temperatures here on Earth which are far too low to give protons and neutrons enough energy to go "over the wall". (In case you are wondering, the reason the same thing does not happen with the electrons in an atom is that the force binding the electrons to the nucleus falls off too slowly with distance, hence there is no region outside the atom which is classically allowed -- there is no place for the electron to tunnel to! However the electron can tunnel in to the nucleus, and this phenomenon, called K-shell capture, is a mode of radioactive decay for certain atoms.)
Tunneling is thought to be important to the function of certain enzymes in the body, and, according to Hawking, may hold the key to how the universe itself came into being (the idea seems to be that the state of no universe is classically allowed, as is the state of an expanding universe of a finite size, but there is no "classical" way to get between the two situations. The solution to the problem of Where Did the Universe Come From might be simply that it tunneled out of nonexistence.)