If you saw nothing on the previous page, then your browser does not
support Java applets.
Otherwise, you found yourself at the controls of a simple simulation of
a binary chemical reaction. There are four types of molecules in
this simulation, red, yellow, green and blue. A pair of
red and yellow molecules if they collide
may react to form a pair of green and blue molecules, and vice versa.
This chemical reaction would be written like so:
R + Y 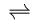 G + B
The central double arrow in this reaction indicates that both the
forward (R + Y --> B + G) and reverse
(B + G --> R + Y) reactions are in principle possible.
This is true of all chemical reactions. However, as is also true of
all chemical reactions, the probability of reaction
during each collision, abbreviated "k",
is not necessarily the same for the forward and reverse reactions.
G + B
The central double arrow in this reaction indicates that both the
forward (R + Y --> B + G) and reverse
(B + G --> R + Y) reactions are in principle possible.
This is true of all chemical reactions. However, as is also true of
all chemical reactions, the probability of reaction
during each collision, abbreviated "k",
is not necessarily the same for the forward and reverse reactions.
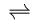 G + B
G + B